Python... Python... part 2
Welcome back...
Now we will continue with part 2 of python programme.
In this post, we will mostly apply what we learnt in part 1.
LET'S BEGIN...
In order to load our inflammation data, we need to access (import in Python terminology) a library called NumPy. In general you should use this library if you want to do fancy things with numbers, especially if you have matrices or arrays. We can import NumPy using:
Libraries provide additional functionality to the basic Python package. Once you’ve imported the library, we can ask the library to read our data file for us:
The expression
When we are finished typing and press Shift+Enter, the notebook runs our command. Since we haven’t told it to do anything else with the function’s output, the notebook displays it. In this case, that output is the data we just loaded. By default, only a few rows and columns are shown (with
Our call to
The line below assigns the value
Once a variable has a value, we can print it to the screen:
and do arithmetic with it:
As the example above shows, we can print several things at once by separating them with commas.
We can also change a variable’s value by assigning it a new one:
This means that assigning a value to one variable does not change the values of other variables. For example, let’s store the subject’s weight in pounds in a variable:
and then change
Since
This statement doesn’t produce any output because assignment doesn’t display anything. If we want to check that our data has been loaded, we can print the variable’s value:
Now that our data is in memory, we can start doing things with it. First, let’s ask what type of thing
The output tells us that
This tells us that
If we want to get a single number from the array, we must provide an index in square brackets, just as we do in math:
The expression
The slice
We don’t have to start slices at 0:
We also don’t have to include the upper and lower bound on the slice. If we don’t include the lower bound, Python uses 0 by default; if we don’t include the upper, the slice runs to the end of the axis, and if we don’t include either (i.e., if we just use ‘:’ on its own), the slice includes everything:
Arrays also know how to perform common mathematical operations on their values. The simplest operations with data are arithmetic: add, subtract, multiply, and divide. When you do such operations on arrays, the operation is done on each individual element of the array. Thus:
will create a new array
If, instead of taking an array and doing arithmetic with a single value (as above) you did the arithmetic operation with another array of the same shape, the operation will be done on corresponding elements of the two arrays. Thus:
will give you an array where
Often, we want to do more than add, subtract, multiply, and divide values of data. NumPy knows how to do more complex operations on arrays. If we want to find the average inflammation for all patients on all days, for example, we can ask NumPy to compute
Everything in a line of code following the ‘#’ symbol is a comment that is ignored by the computer. Comments allow programmers to leave explanatory notes for other programmers or their future selves.
We don’t actually need to store the row in a variable of its own. Instead, we can combine the selection and the function call:
What if we need the maximum inflammation for each patient over all days (as in the next diagram on the left), or the average for each day (as in the diagram on the right)? As the diagram below shows, we want to perform the operation across an axis:
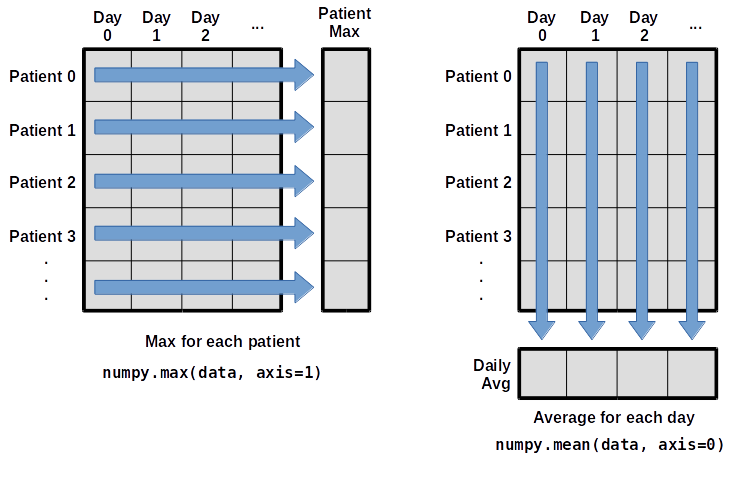
To support this, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
As a quick check, we can ask this array what its shape is:
The expression
which is the average inflammation per patient across all days.
Now, we will explore a few features of Python’s

Blue regions in this heat map are low values, while red shows high values. As we can see, inflammation rises and falls over a 40-day period.

Here, we have put the average per day across all patients in the variable


The maximum value rises and falls perfectly smoothly, while the minimum seems to be a step function. Neither result seems particularly likely, so either there’s a mistake in our calculations or something is wrong with our data. This insight would have been difficult to reach by examining the data without visualization tools.
You can group similar plots in a single figure using subplots. This script below uses a number of new commands. The function

The call to
That's all for part 2...
Now we will continue with part 2 of python programme.
In this post, we will mostly apply what we learnt in part 1.
LET'S BEGIN...
In order to load our inflammation data, we need to access (import in Python terminology) a library called NumPy. In general you should use this library if you want to do fancy things with numbers, especially if you have matrices or arrays. We can import NumPy using:
import numpy
Libraries provide additional functionality to the basic Python package. Once you’ve imported the library, we can ask the library to read our data file for us:
numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')
array([[ 0., 0., 1., ..., 3., 0., 0.],
[ 0., 1., 2., ..., 1., 0., 1.],
[ 0., 1., 1., ..., 2., 1., 1.],
...,
[ 0., 1., 1., ..., 1., 1., 1.],
[ 0., 0., 0., ..., 0., 2., 0.],
[ 0., 0., 1., ..., 1., 1., 0.]]) numpy.loadtxt(...) is a function call that asks Python to run the function loadtxt which belongs to the numpy library. This dotted notation is used everywhere in Python to refer to the parts of things as thing.component.numpy.loadtxt has two parameters: the name of the file we want to read, and the delimiter that separates values on a line. These both need to be character strings (or strings for short), so we put them in quotes.When we are finished typing and press Shift+Enter, the notebook runs our command. Since we haven’t told it to do anything else with the function’s output, the notebook displays it. In this case, that output is the data we just loaded. By default, only a few rows and columns are shown (with
... to omit elements when displaying big arrays).Our call to
numpy.loadtxt read our file, but didn’t save the data in memory. To do that, we need to assign the array to a variable. A variable is just a name for a value, such as x, current_temperature, or subject_id. Python’s variables must begin with a letter and are case sensitive. We can create a new variable by assigning a value to it using =. To illustrate, continue below.The line below assigns the value
55 to a variable weight_kg: weight_kg = 55
Once a variable has a value, we can print it to the screen:
print(weight_kg)
Output 55
and do arithmetic with it:
print('weight in pounds:', 2.2 * weight_kg)
weight in pounds: 121.0
As the example above shows, we can print several things at once by separating them with commas.
We can also change a variable’s value by assigning it a new one:
weight_kg = 57.5
print('weight in kilograms is now:', weight_kg)
weight in kilograms is now: 57.5
This means that assigning a value to one variable does not change the values of other variables. For example, let’s store the subject’s weight in pounds in a variable:
weight_lb = 2.2 * weight_kg
print('weight in kilograms:', weight_kg, 'and in pounds:', weight_lb)
weight in kilograms: 57.5 and in pounds: 126.5 and then change
weight_kg:weight_kg = 100.0
print('weight in kilograms is now:', weight_kg, 'and weight in pounds is still:', weight_lb)
weight in kilograms is now: 100.0 and weight in pounds is still: 126.5
Since
weight_lb doesn’t “remember” where its value came from, it isn’t automatically updated when weight_kg changes. This is different from the way spreadsheets work.Who’s Who in Memory
You can use the%whoscommand at any time to see what variables you have created and what modules you have loaded into the computer’s memory. As this is an IPython command, it will only work if you are in an IPython terminal or the Jupyter Notebook.
Just as we can assign a single value to a variable, we can also assign an array of values to a variable using the same syntax. Let’s re-run%whosVariable Type Data/Info -------------------------------- numpy module <module 'numpy' from '/Us<...>kages/numpy/__init__.py'> weight_kg float 100.0 weight_lb float 126.5
numpy.loadtxt and save its result:data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',') print(data)
[[ 0. 0. 1. ..., 3. 0. 0.]
[ 0. 1. 2. ..., 1. 0. 1.]
[ 0. 1. 1. ..., 2. 1. 1.]
...,
[ 0. 1. 1. ..., 1. 1. 1.]
[ 0. 0. 0. ..., 0. 2. 0.]
[ 0. 0. 1. ..., 1. 1. 0.]] data refers to:print(type(data))
<class 'numpy.ndarray'> data currently refers to an N-dimensional array created by the NumPy library. These data correspond to arthritis patients’ inflammation. The rows are the individual patients and the columns are their daily inflammation measurements.Data Type
A Numpy array contains one or more elements of the same type.typewill only tell you that a variable is a NumPy array. We can also find out the type of the data contained in the NumPy array.
print(data.dtype)dtype('float64')
This tells us that the NumPy array’s elements are floating-point numbers.We can see what the array’s shape is like this:
print(data.shape)
(60, 40) data has 60 rows and 40 columns. When we created the variable data to store our arthritis data, we didn’t just create the array, we also created information about the array, called members or attributes. This extra information describes data in the same way an adjective describes a noun. data.shape is an attribute of data which describes the dimensions of data. We use the same dotted notation for the attributes of variables that we use for the functions in libraries because they have the same part-and-whole relationship.If we want to get a single number from the array, we must provide an index in square brackets, just as we do in math:
print('first value in data:', data[0, 0])
first value in data: 0.0
print('middle value in data:', data[30, 20])
middle value in data: 13.0 data[30, 20] may not surprise you, but data[0, 0] might. Languages in the C family (including C++, Java, Perl, and Python) count from 0 because it represents an offset from the first value in the array (the second value is offset by one index from the first value). This is closer to the way that computers represent arrays. As a result, if we have an M×N array in Python, its indices go from 0 to M-1 on the first axis and 0 to N-1 on the second. It takes a bit of getting used to, but one way to remember the rule is that the index is how many steps we have to take from the start to get the item we want.An index likeIn the Corner
What may also surprise you is that when Python displays an array, it shows the element with index[0, 0]in the upper left corner rather than the lower left. This is consistent with the way mathematicians draw matrices, but different from the Cartesian coordinates. The indices are (row, column) instead of (column, row) for the same reason, which can be confusing when plotting data.
[30, 20] selects a single element of an array, but we can select whole sections as well. For example, we can select the first ten days (columns) of values for the first four patients (rows) like this:print(data[0:4, 0:10])
[[ 0. 0. 1. 3. 1. 2. 4. 7. 8. 3.]
[ 0. 1. 2. 1. 2. 1. 3. 2. 2. 6.]
[ 0. 1. 1. 3. 3. 2. 6. 2. 5. 9.]
[ 0. 0. 2. 0. 4. 2. 2. 1. 6. 7.]] 0:4 means, “Start at index 0 and go up to, but not including, index 4.” Again, the up-to-but-not-including takes a bit of getting used to, but the rule is that the difference between the upper and lower bounds is the number of values in the slice.We don’t have to start slices at 0:
print(data[5:10, 0:10])
[[ 0. 0. 1. 2. 2. 4. 2. 1. 6. 4.]
[ 0. 0. 2. 2. 4. 2. 2. 5. 5. 8.]
[ 0. 0. 1. 2. 3. 1. 2. 3. 5. 3.]
[ 0. 0. 0. 3. 1. 5. 6. 5. 5. 8.]
[ 0. 1. 1. 2. 1. 3. 5. 3. 5. 8.]] small = data[:3, 36:]
print('small is:')
print(small)
small is:
[[ 2. 3. 0. 0.]
[ 1. 1. 0. 1.]
[ 2. 2. 1. 1.]] doubledata = data * 2.0
doubledata whose elements have the value of two times the value of the corresponding elements in data:print('original:')
print(data[:3, 36:])
print('doubledata:')
print(doubledata[:3, 36:])
original:
[[ 2. 3. 0. 0.]
[ 1. 1. 0. 1.]
[ 2. 2. 1. 1.]]
doubledata:
[[ 4. 6. 0. 0.]
[ 2. 2. 0. 2.]
[ 4. 4. 2. 2.]] tripledata = doubledata + data tripledata[0,0] will equal doubledata[0,0] plus data[0,0], and so on for all other elements of the arrays.print('tripledata:')
print(tripledata[:3, 36:])
tripledata:
[[ 6. 9. 0. 0.]
[ 3. 3. 0. 3.]
[ 6. 6. 3. 3.]] data’s mean value:print(numpy.mean(data))
6.14875
mean is a function that takes an array as an argument. If variables are nouns, functions are verbs: they do things with variables.Not All Functions Have Input
Generally, a function uses inputs to produce outputs. However, some functions produce outputs without needing any input.
import time print(time.ctime())'Sat Mar 26 13:07:33 2016'
NumPy has lots of useful functions that take an array as input. Let’s use three of those functions to get some descriptive values about the dataset. We’ll also use multiple assignment, a convenient Python feature that will enable us to do this all in one line.For functions that don’t take in any arguments, we still need parentheses (()) to tell Python to go and do something for us.
maxval, minval, stdval = numpy.max(data), numpy.min(data), numpy.std(data)
print('maximum inflammation:', maxval)
print('minimum inflammation:', minval)
print('standard deviation:', stdval)
maximum inflammation: 20.0
minimum inflammation: 0.0
standard deviation: 4.61383319712
When analyzing data, though, we often want to look at partial statistics, such as the maximum value per patient or the average value per day. One way to do this is to create a new temporary array of the data we want, then ask it to do the calculation:Mystery Functions in IPython
patient_0 = data[0, :] # 0 on the first axis, everything on the second
print('maximum inflammation for patient 0:', patient_0.max())
maximum inflammation for patient 0: 18.0 We don’t actually need to store the row in a variable of its own. Instead, we can combine the selection and the function call:
print('maximum inflammation for patient 2:', numpy.max(data[2, :]))
maximum inflammation for patient 2: 19.0 
To support this, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
print(numpy.mean(data, axis=0))
[ 0. 0.45 1.11666667 1.75 2.43333333 3.15
3.8 3.88333333 5.23333333 5.51666667 5.95 5.9
8.35 7.73333333 8.36666667 9.5 9.58333333
10.63333333 11.56666667 12.35 13.25 11.96666667
11.03333333 10.16666667 10. 8.66666667 9.15 7.25
7.33333333 6.58333333 6.06666667 5.95 5.11666667 3.6
3.3 3.56666667 2.48333333 1.5 1.13333333
0.56666667]
As a quick check, we can ask this array what its shape is:
print(numpy.mean(data, axis=0).shape)
(40,) (40,) tells us we have an N×1 vector, so this is the average inflammation per day for all patients. If we average across axis 1 (columns in our 2D example), we get:print(numpy.mean(data, axis=1)) [ 5.45 5.425 6.1 5.9 5.55 6.225 5.975 6.65 6.625 6.525
6.775 5.8 6.225 5.75 5.225 6.3 6.55 5.7 5.85 6.55
5.775 5.825 6.175 6.1 5.8 6.425 6.05 6.025 6.175 6.55
6.175 6.35 6.725 6.125 7.075 5.725 5.925 6.15 6.075 5.75
5.975 5.725 6.3 5.9 6.75 5.925 7.225 6.15 5.95 6.275 5.7
6.1 6.825 5.975 6.725 5.7 6.25 6.4 7.05 5.9 ] Now, we will explore a few features of Python’s
matplotlib library here. While there is no “official” plotting library, this package is the de facto standard. First, we will import the pyplot module from matplotlib and use two of its functions to create and display a heat map of our data:import matplotlib.pyplot
image = matplotlib.pyplot.imshow(data)
matplotlib.pyplot.show() 
Blue regions in this heat map are low values, while red shows high values. As we can see, inflammation rises and falls over a 40-day period.
Some IPython Magic
If you’re using an IPython / Jupyter notebook, you’ll need to execute the following command in order for your matplotlib images to appear in the notebook whenshow()is called:
% matplotlib inline
Let’s take a look at the average inflammation over time:The%indicates an IPython magic function - a function that is only valid within the notebook environment. Note that you only have to execute this function once per notebook.
ave_inflammation = numpy.mean(data, axis=0)
ave_plot = matplotlib.pyplot.plot(ave_inflammation)
matplotlib.pyplot.show()

Here, we have put the average per day across all patients in the variable
ave_inflammation, then asked matplotlib.pyplot to create and display a line graph of those values. The result is roughly a linear rise and fall, which is suspicious: based on other studies, we expect a sharper rise and slower fall. Let’s have a look at two other statistics:max_plot = matplotlib.pyplot.plot(numpy.max(data, axis=0))
matplotlib.pyplot.show()

min_plot = matplotlib.pyplot.plot(numpy.min(data, axis=0))
matplotlib.pyplot.show() 
The maximum value rises and falls perfectly smoothly, while the minimum seems to be a step function. Neither result seems particularly likely, so either there’s a mistake in our calculations or something is wrong with our data. This insight would have been difficult to reach by examining the data without visualization tools.
You can group similar plots in a single figure using subplots. This script below uses a number of new commands. The function
matplotlib.pyplot.figure() creates a space into which we will place all of our plots. The parameter figsize tells Python how big to make this space. Each subplot is placed into the figure using its add_subplot method. The add_subplot method takes 3 parameters. The first denotes how many total rows of subplots there are, the second parameter refers to the total number of subplot columns, and the final parameter denotes which subplot your variable is referencing (left-to-right, top-to-bottom). Each subplot is stored in a different variable (axes1, axes2, axes3). Once a subplot is created, the axes can be titled using the set_xlabel() command (or set_ylabel()). Here are our three plots side by side:import numpy
import matplotlib.pyplot
data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')
fig = matplotlib.pyplot.figure(figsize=(10.0, 3.0))
axes1 = fig.add_subplot(1, 3, 1)
axes2 = fig.add_subplot(1, 3, 2)
axes3 = fig.add_subplot(1, 3, 3)
axes1.set_ylabel('average')
axes1.plot(numpy.mean(data, axis=0))
axes2.set_ylabel('max')
axes2.plot(numpy.max(data, axis=0))
axes3.set_ylabel('min')
axes3.plot(numpy.min(data, axis=0))
fig.tight_layout()
matplotlib.pyplot.show()

The call to
loadtxt reads our data, and the rest of the program tells the plotting library how large we want the figure to be, that we’re creating three subplots, what to draw for each one, and that we want a tight layout. (Perversely, if we leave out that call to fig.tight_layout(), the graphs will actually be squeezed together more closely.)That's all for part 2...
Comments
Post a Comment